Gene expression synthesis is a way to evolve sound synthesizers in computer code. These synthesizers are computer programs that produce sound when executed. Gene expression synthesis uses the methods of gene expression programming proposed by Candida Ferreira in 2001. Gene expression programming combines ideas from the two most widely used and well-known evolutionary programming methods: genetic algorithms and genetic programming. Genetic algorithms encode solutions to programming problems as linear strings of digits, typically binary, while genetic programming evolves computer programs as tree structres in which every computer function or parameter value is represented as a node. Gene expression programming does both: the solutions are encoded as linear strings which are decoded into tree structures representing computer programs. Each candidate solution in a population of computer programs is subjected to a fitness evaluation that determines how well a particular program performs in solving a target problem. I have developed gene expression synthesis in the SuperCollider programming environment. A paper on gene expression synthesis appeared in the proceedings of the International Computer Music Conference 2014 and is available as PDF.

Since the first artificial life experiments by Nils A. Barricelli in the 1950s, evolutionary computing has inspired numerous problem solving and model building techniques including ways to evolve sound synthesis algorithms inspired by processes of evolution by adaptation and natural selection. In our attempts to understand these natural algorithmic processes, which are purposeless and devoid of any intention, but nonetheless directly responsible for all the complexity and intelligent behavior in the natural world, we keep developing increasingly more powerful technology that enables us to model and simulate, albeit on a vastly simplified scale, the power of cumulative selection. Genetic algorithms and genetic programming have been firmly established as efficient and productive stochastic search and optimization methods within the artificial intelligence field and have been widely used in various disciplines for years. Gene expression programming was introduced as an improvement to the existing paradigms by combining the best features of genetic algorithms and genetic programming. The fundamental differences between gene expression programming and its predecessors stem from the separation of genotype-phenotype representations and the modular multigenic structure of the chromosomes. These improvements account for significant increases to the efficiency of the algorithm for a number of benchmark problems. The following account describes an experimental approach to evolving sound generating programs with the proposed principles and explores creative applications of evolutionary computation which do not necessarily presume a definite solution to a problem, but rather an open-ended solution space to be explored for aesthetic experimentation.

The evolutionary paradigm has been harnessed in a broad spectrum of applications in the realm of computer music, applying the processes of gene expression, selection, reproduction and variation on many different levels of compositional hierarchy. Examples can be drawn throughout all musical time levels, including producing waveforms directly by expressing binary genotypes as sample level time functions, evolving synthesis graphs and optimizing parameters, generating longer time structures and patterns of motives and phrases, all the way to composing comprehensive artificial environments inhabited by listening and sound-generating agents. Cristyn Magnus developed a modified genetic algorithm that works directly on time-domain waveforms to produce genetically evolved electroacoustic music. On the phrase and motive level, there are two classic studies that paved the way for countless later explorations: John Biles hierarchical GenJam system that generates on-the-fly jazz chord progressions and the "sonomorphs" proposed by Gary Lee Nelson. Jon McCormack developed Eden, an interactive installation of evolving agents influenced by the presence and movement of audience as an example of a comprehensive digital sonic ecosystem. These are but a few examples of the wide range of applications for evolutionary algorithms and by no means meant as a review, rather a random sampling of applications on different levels of the compositional process. A similar approach to the one presented here was developed by Ricardo Garcia who proposed using evolutionary methods for selecting topological arrangements of sound synthesis algorithms and automating the fitness evaluation by audio feature comparison.

The abundance of different possibilities explored demonstrates the potential inherent in evolutionary processes which can exhibit unparalleled efficiency and problem-solving resourcefulness even in a vastly simplified form as compared to the forces operating in the natural world. The idea of automating the design process of sound synthesis algorithms using evolutionary methods has to be considered in the context of computer music specification. Generating waveforms by the direct principle of sample-by-sample calculation, for example, does not necessarily require any higher level infrastructure or a specialized programming environment, however, such an approach may complicate the design of an efficient fitness function, especially considering unsupervised learning methods. Since the Music N programming languages (most prominently Csound), the encapsulation of sound generating and processing functions into unit generators has cultivated a modular graph based concept of synthesis with interconnectable functions as building blocks. Most contemporary synthesis software, regardless of whether the interface is graphical or text-based, operates based on this model. The method presented here has been implemented in the SuperCollider environment, but is applicable in any audio programming environment that has adopted the graph based paradigm, where sound synthesis programs are defined as interconnected unit generator graphs. These graphs can be evolved by evolutionary programming principles just like any other computer programs that serve as the solution space for a particular problem. The question then becomes how to define or, in other words, encode these graphs in terms of evolutionary programming.

SuperCollider synthesis topologies have previously been studied in the context of evolutionary programming. Dan Stowell presented a genetic algorithm for live audio evolution at the first SuperCollider symposium in Birmingham 2006. The system demonstrates how genetic methods can be used in a live setting, with modifications to the synthesis process occurring in real time. Fredrik Olofsson released a similar algorithm for sound synthesis through his personal website. The goal of his project was to create genomes that would translate into realtime synthesis processes and allow the user to evaluate the results in a framework of a realtime sequencer. The algorithm is, similarly to the one described above, based on arrays of floating point values serving as genomes, which were translated into SuperCollider synthesis definitions.

The SuperCollider implementation of the gene expression programming proposed here expands on the foundations of the methods described above. The problem addressed is how to encode SuperCollider unit generator graphs as populations of chromosomes and evolve these graphs using genetic operators. In a similar way, there is a constrained selection of unit generators that are included in the graphs and the translation process produces valid sound generating functions that are evaluated for fitness. However, the following description introduces a number of modifications and distinct features in accordance with the techniques of the gene expression algorithm to introduce an alternative strategy for evolutionary sound synthesis.

Gene expression programming (GEP) is a method of evolutionary computation providing an alternative to the established paradigms of classic genetic algorithms (GA) and genetic programming (GP). The basic premises that these methods share in common have been inspired by biological evolution and attempt to model the natural selection process algorithmically in computers. All these methods use populations of individuals as potential solutions to a defined problem, select the individuals from generation to generation according to fitness, and propagate genetic variation within the population by random initiation and applying genetic operators. The differences between these algorithms are defined by the nature of individuals. In GAs the individuals are fixed length strings of numbers (traditionally binary); in GP the individuals are non-linear tree structures of different sizes and levels of complexity. GEP combines these approaches by encoding complex expression trees as simple strings of fixed length to overcome the inherent limitations of the previous methods. In GEP the genotype and phenotype are expressed as separate entities, the structure of the chromosome allowing to represent any expression tree which always produces a valid computer program. Another feature to set GEP apart from its predecessors is the structural design of GEP individuals that allows encoding multiple genes in a single chromosome. This facilitates encoding programs of higher complexity and expands the range of problems that can be solved with evolutionary computing.

GEP consists of two principal components: the genes (genotype) and the expression trees (the phenotype). The information decoding from chromosomes to expression trees is called translation. The genome or chromosome consists of a linear, symbolic string of fixed length composed of one or more genes. Each gene is structurally divided into two sections: a head and a tail. There are two types of codons that make up a gene: ones that designate computer functions and terminals which operate as placeholders for static variables or arguments to the functions. The head of a gene contains symbols representing both functions and terminals with the start codon always holding a function while the tail is entirely made up of terminals. This structure and the particular rules of translation in GEP ensure that each gene encodes a valid computer program. Despite the fixed length of the genome, each gene has the potential to encode for expression trees of different levels of complexity and nesting. The translation from genotype to phenotype follows a simple, breadth-first recursive principle: as the codons of a gene are traversed, for each function encountered, the algorithm reserves a number of following unreserved codons as arguments to that function regardless whether they are functions or terminals. The number of codons reserved depends on the number of arguments the function encountered requires. In order to illustrate this process, encoding of a simple phase modulation graph is shown in this figure.

Such a gene would have to consists of a head section with at least 3 codons and tail with at least 6. The first 3 positions in the head of this gene contain the two sine oscillator functions and a terminal in between (the head part of the gene is indicated by a shaded grey background). The tail is entirely made up of terminals.

In the Karva notation this chromosome is represented as a string of upper and lower case letters with position reference numbers above:

The expression tree that emerges form this gene after the translation process looks like this:

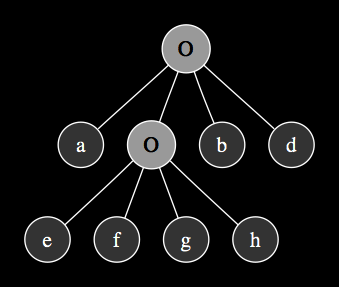
The first codon designating a SinOsc ar method (represented here by symbol O) - which in SuperCollider language specification expects four arguments: frequency, phase, mul and add - is translated as the root node in the expression tree with four branches deriving their values from codons in positions 1 to 4 in the chromosome string as they get reserved according to number of arguments into the function. When the algorithm encounters a terminal, there is no need to reserve anything and the terminal is assigned its position in the tree with no further branching, however, when it comes across another function at position 2 in the head of the gene, it looks ahead to reserve the next sequence of codons, in this case four arguments are expected again, therefore terminals at positions 5 to 8 fill these nodes. Once the algorithm has filled all the function arguments, the process stops and the rest of the terminals in the tail section of the gene are ignored. This mechanism allows to define the potential complexity and nesting in the resulting computer programs as a function of overall gene length. The expression tree above translates into a corresponding SuperCollider unit generator graph function:

{arg a, b, c, d, e, f, g;
	SinOsc.ar(a, SinOsc.ar(d, e, f, g), b, c) 
}

The size of the gene tail t is calculated based on the size of the head h and the number of terminals n required by the function with the largest number of arguments:

t=h(n-1)+1

Another feature that sets GEP apart from other evolutionary algorithms is the use of multigenic chromosomes. Multigenic chromosomes can be combined together by a function that serves as a linker. In order to provide an example of a multigenic chromosome, let us consider a slightly more complex example than the phase modulation graph above. This time there are four unit generators involved: sine oscillator SinOsc (O), sawtooth wave oscillator LFSaw (S), random values oscillator with quadratic interpolation LFNoise2 (N) and band-limited pulse wave generator Pulse (P). Since the generator with largest number of arguments is the sine tone oscillator and the head size remains the same for the time being, the gene size is also the same as above, but this time the chromosome consists of two genes which are linked together by mathematical multiplication function in the translation process. The gene expression tree of this chromosome consists of two independent sub expression trees corresponding to the multigenic structure: the first one has a noise generator as the root codon and the second one a sawtooth oscillator. There is an additional linker function, in this case multiplication, which combines the genes together into a single composite function:

This expression tree translates to a unit generator graph function in SuperCollider:

{arg a,b,c,d,e,f,g,h;
	LFNoise2.ar(
		SinOsc.ar(a,d,c,c),
		SinOsc.ar(d,h,e,c),
	g) *
	LFSaw.ar(
		Pulse.ar(h, f, b ),
		f, d, a
	)
}

GEP chromosomes contain several genes each coding for structurally and functionally unique expression trees. Depending on the problem to be solved, these sub-trees may be selected individually according to their respective fitness or they may form a more complex multi-subunit expression tree and be selected according to the fitness of the whole chromosome. The linker between the individual expression trees can also be any function and depends on the context of the task at hand. For example, in the above structure, the multiplication could be substituted by addition to produce additive synthesis instead of modulation synthesis or any other function that requires two arguments.

The gene expression process does not differ much from that of the classic genetic algorithms. It begins with the random generation of chromosomes of a certain number of individuals for the initial population. In the next step, these chromosomes are translated into computer functions to be executed and the fitness of each individual is assessed against a set of desired examples which act as the environment to which the individuals are to be adapted. The individuals are then selected according to their fitness (their performance in that particular environment) to reproduce with modification, leaving progeny with new traits. These new individuals are, in their turn, subjected to the same developmental process: expression of the genomes, confrontation of the selection environment, selection, and reproduction with modification. The process is repeated for a certain number of generations or until a good solution has been found.

The initial population in gene expression programming is created in the same way as in other evolutionary computation algorithms either by randomly populating the gene codons with functions and terminals determined to be part of the solution space or using pre-existing individuals from a pool of previous successful runs. In case of random generation of the population, which is by far the most common method used, the genes are constructed, first, by randomly selecting a root node from the included function definitions, then the head codons are filled by randomly selecting a function or a terminal for each position and, finally, the tail only includes random selections of terminal values. Although, it is not absolutely necessary to define a root node as a function according to GEP principles, especially in multigenic chromosomes, however it proves more crucial of a factor in the special case of sound synthesis. Sound synthesis is a special case for more than one reason and the many constraints that it imposes on the GEP paradigm will be discussed in detail in the following sections.

As in any other evolutionary programming model, the most important and challenging component in GEP is the design of the fitness cases as this is what drives the fitness of the population and ultimately decides the success of the problem solving algorithm. In most cases which are trying to find the single best solution to a particular problem, the goal must be defined clearly and precisely in order for the system to evolve in the intended direction. Although it may not always be the case, particularly while evolving candidate solutions for complex, open-ended situations including sound synthesis or musical phrase composition, a poorly designed fitness function tends to produce random meaningless results and either converges on an inappropriate solution or will not converge at all producing consistently large error values in individuals with the highest fitness.

The selection process commences once each individual in the population has been assigned a fitness value. The purpose of this phase of the algorithm is to propagate the fittest solutions to the following generation. Again, there are a number of different methods by which to select the individuals, stochastic and deterministic, however in the long run it makes little difference which one is used as long as the best traits of the current population are preserved in the new population. The preferred method in GEP is stochastic, which entails assigning each chromosome in the population a probability weight value proportional to its relative fitness. This may mean that the fittest individual may not always survive the selection process while mediocre individuals might be selected.

The selection process has a tendency to converge towards a single high scoring solution and, without genetic operators, would rapidly get stuck in a local optimum. Therefore it is essential to maintain genetic diversity, which is mainly achieved by several modifications introduced during the replication process of the genomes. There are a variety of genetic operators in GEP divided into three main categories: mutation, transposition, recombination.

Mutation entails modifying a single value in a randomly chosen position and can occur anywhere in the chromosome. However, the structural organization of the chromosome must be preserved to ensure that when expressed the individual still produces a valid program. This means that the root can only be replaced by another function, any codon in the head section of the chromosome can be substituted by a function or a terminal and only terminals are allowed as replacements in the tail section. Mutations of a single codon can have a dramatic effect on the phenotype a chromosome is encoding, especially if it occurs in the head section. The following Karva notation strings display a mutated chromosome before and after the mutation, in which a terminal that occurs in position 1 in the original gene has mutated into a sine oscillator in the next generation:

Here is the effect on corresponding expression trees of this single-point mutation:

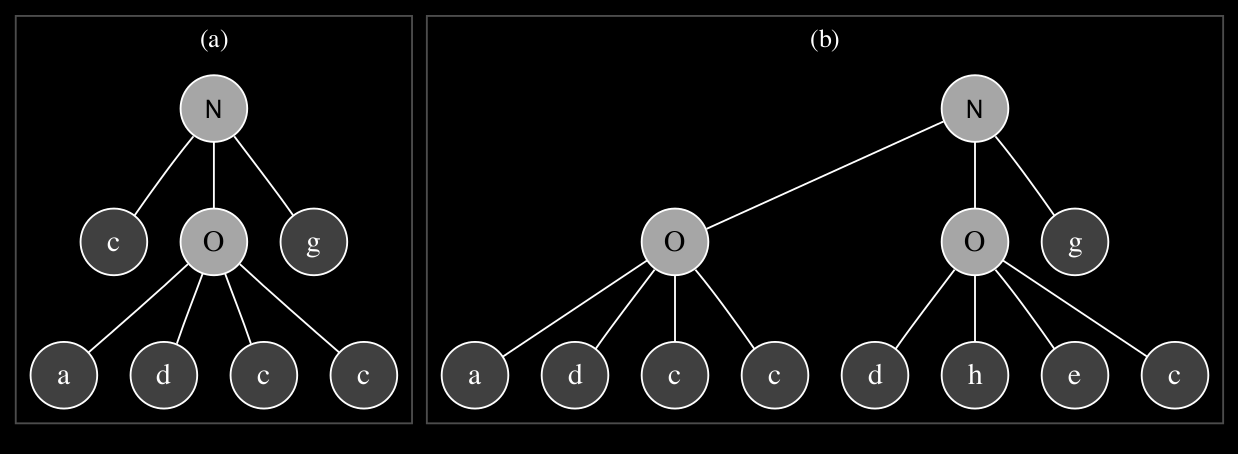
Mutation rate is defined as a global constant in the GEP algorithm and can be specified as a probability percentage which each chromosome is subjected to. If the mutation rate is defined as 0.1, it means each chromosome has a 10\% chance of being subject to a random one-point mutation.

The transposition operations in GES copy short fragments of the genome from their original locations to another location in the chromosome. For example the already familiar gene from two previous examples is subjected to transposition of a short codon sequence shown in Karva notation.

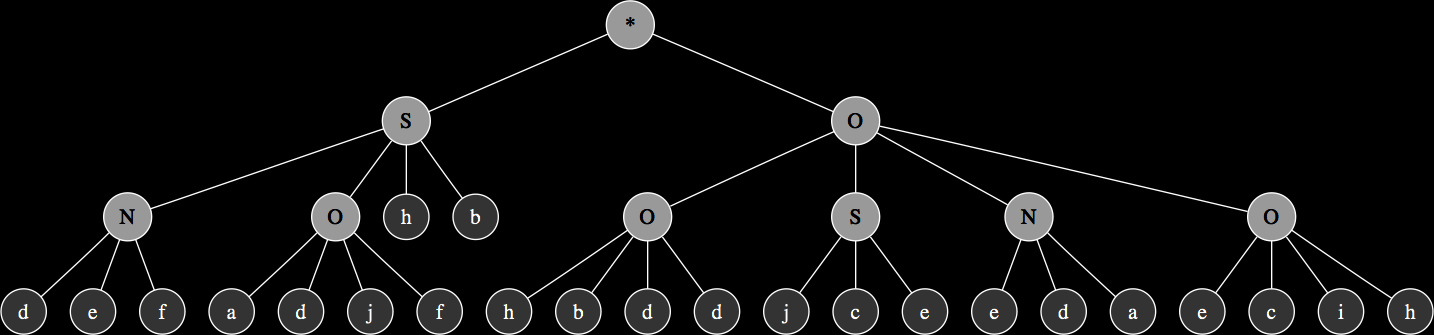
The terminals at locations 5 and 6 are copied into the head section of the gene, which results in the first two parameters - frequency and phase in this case - of the root codon sawtooth oscillator of the first gene to be replaced by a noise generator and a terminal instead of a sine oscillator and a noise generator. The SuperCollider synthesis function that is derived from the transposed tree is shown in the code listing below:

SynthDef('r00_g02_s001', {arg a,b,c,d,e,f,g,h,i;
	Out.ar(0, (
		LFSaw.ar(
			SinOsc.ar(e,f,a,d),
			LFNoise2.ar(i,f,a),
			SinOsc.ar(a,h,f,f),
			d
		)
	) * (
		LFNoise2.ar(
			LFNoise2.ar(b,d,d),
			h,
			SinOsc.ar(i,c,e,e)
		)
	)
  )
})

Recombination involves choosing chromosomes from the pool of individuals that have successfully passed the selection process and exchanging their genetic material. This process results in creation of two new individuals. A defined number of points are randomly chosen along the two parents and their codons are copied to the child chromosomes as mixed set containing codons from each of the parents. In order to illustrate the basic principles and effects of recombination let us consider two chromosomes derived from the same four unit generators presented previously. The listings below display two parent chromosomes in Karva notation (head sections in bold):

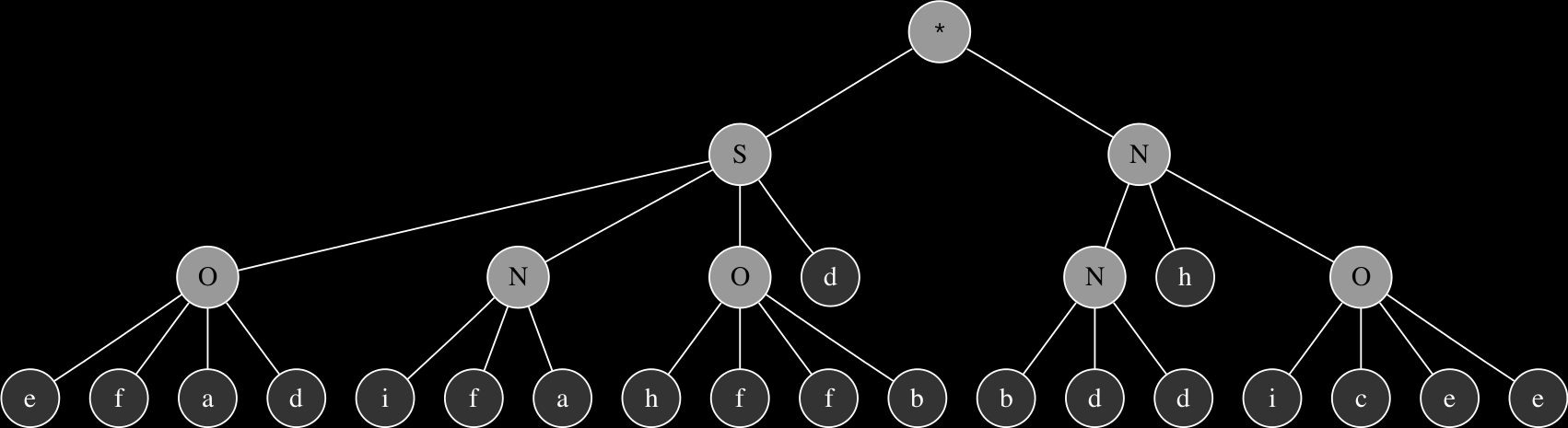
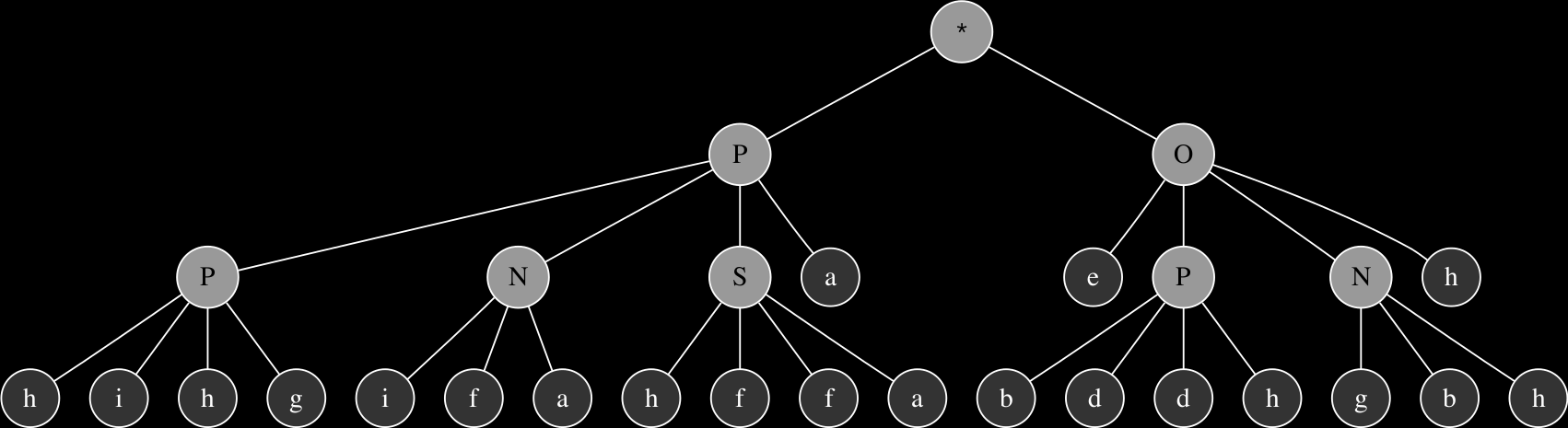
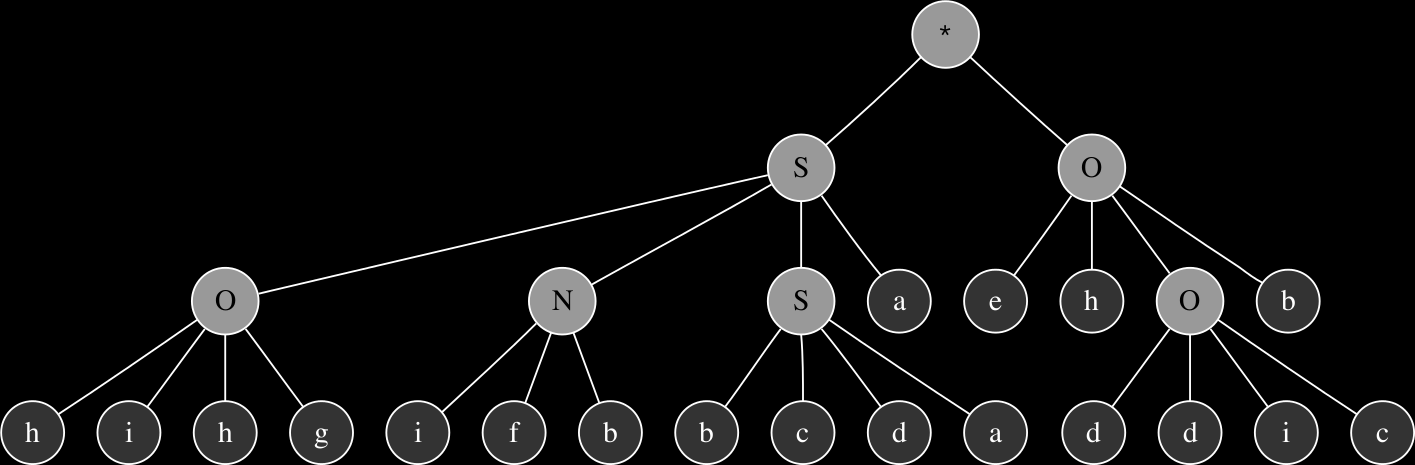
After subjecting these chromosomes to recombination, the result is two new individuals that have characteristics of each of the parents. In the symbol strings below, the components that made up the original chromosome 1 are indicated in bold to illustrate the effect of recombination. The first of the two randomly selected recombination points is located at position 3 of the chromosome and the second occurred at position 27 located in the head section of the second gene.
The corresponding expression trees of the two parents and their progeny:

These are relatively simple examples in order to demonstrate the principles of genetic operations in gene expression synthesis. The synthesis functions that have been evolved so far using this technique typically originate from chromosomes consisting of at least 4 up to 8 genes and head sizes ranging between 8 to 16, resulting in much more complex graphs with more levels of nesting. While the genetic operations ensure variability within the population, evolution towards a goal is largely determined by a fitness function.

The fitness function uses machine listening algorithms to analyze the candidate solutions once they have passed an initial basic compilation test on the SuperCollider server. Before the machine analysis can commence, any individual that fails the basic fitness check and the expressed function fails to compile, is automatically assigned a weight value of 0 and consequently excluded from the selection process. Compilation may fail for any number of reasons, the most common being invalid input type and since initialization is completely random, unsuitable function arguments become quite frequent in case unit generators that have arguments of specific type. A good example of an invalid unit generator argument would be in case of a filter algorithm which expects the first argument to be a signal of the same rate (typically audio rate in this case) as it is running itself, therefore a floating point number is not accepted and compilation fails. There is an option to start the process by filling the initial population exclusively with candidate solutions that pass this check.

The machine listening process analyses a set of 20 mel frequency cepstral coefficients (MFCC), spectral flatness, spectral centroid, and amplitude features into running mean and standard deviation values over a desired duration, 3 to 8 seconds in the runs reported in this account. Invalid output from any of the analysis processes (mostly NaN or unrepresentable value as a result of a calculation, dividing 0 by 0 for example) is assigned an error value greater than one which gets treated the same way as uncompilable functions and is thereby excluded from the selection process. The fitness function that was used in all the variants of the gene expression experiments under investigation in this case used example analysis sets extracted from sound examples towards which the algorithm was expected to converge. A number of different reference sounds were used including sounds synthesized with GES, other types of synthesized sounds as well as sounds of traditional musical instruments. The score of each individual was determined as the difference between maximum possible score and the total actual error in each of the analysis categories. The mean and standard deviation statistics of each of the MFC coefficients were given double weighting relative to other statistical values and the maximum error in each of the statistical categories was set to 1.0. Spectral centroid values, which are expressed in frequency values, were mapped to range between 0.0 and 1.0. This meant a maximum individual score of 10.0 as the sum of scores from MFC coefficients adding up to 2.0 for both mean and standard deviation statistics, and to 1.0 for spectral flatness, spectral centroid, and amplitude.

The table below represents the assignment of initial fitness scores which were calculated as difference measures from the corresponding features of the reference sound. Each of the 20 mean MFCC coefficients were each assigned a weight value of 0.1, which means that the maximum score possible from the sum of these features is 2.0. The same weight is assigned to the standard deviation values of MFCC. The remaining 6 features - mean and standard deviation values for Spectral Flatness, Spectral Centroid, and Amplitude - were each assigned a weight of 1.0. Therefore the maximum similarity score possible is 10.0 in case of identical features.

FEATURE	NUMBER	WEIGHT	MAX
MFCC (mean)	20	0.10	2.00
MFCC (std dev)	20	0.10	2.00
Flatness (mean)	1	1.00	1.00
Flatness (std dev)	1	1.00	1.00
Centroid (mean)	1	1.00	1.00
Centroid (std dev)	1	1.00	1.00
Amplitude (mean)	1	1.00	1.00
Amplitude (std dev)	1	1.00	1.00
		Total max	10.00

In order to imitate the condition of limited resources of natural selection, each candidate solution is assigned a CPU usage value measured during the execution of the synthesizer. At the end of each evaluation cycle, the CPU usage percentage is normalized relative to the minimum and maximum values of the population and the scores recalculated adding in the CPU percentage as 10 percent of the total score. This pressure introduces a tendency in the population of favoring simpler synthesizer graphs over more complex ones. To counteract this tendency a conflicting fitness pressure is introduced to encourage structural complexity. Maximum depth of unit generator nesting is a straightforward indicator of complexity in graphs, so the scores are adjusted according to the maximum depth of a chromosome relative to the maximum of the population. This way, the complexity can be maintained in populations, while still encouraging resource usage effectiveness. These parameters can be adjusted depending on the purpose of the experiment.

This tutorial introduces the SuperCollider classes needed to start evolving SynthDefs with gene expression synthesis. All the files necessary are included in the tarball here: ges.tar.gz. This example is provided with the acqkowledgement of the fact that there are many alternative ways to define the parameters and the fitness function for gene expression synthesis, the approach here is just one of those possible and is by no means considered the perfect solution. In order to implement a different fitness function, for example, the one in the GepRun class can be replaced.

If you want to save the results of your experiment, you should create a directory structure to accommodate the save functionality before starting this tutorial. The Paths class included in the tarball handles the paths. Specify Paths.prefix for your user home directory, Paths.gepdir is relative to user home where you want to store the synthesis experiments. This directory contains 3 sub-directories: synthdefs, data and metadata.

The first step is to define the size of head section of each gene and the number of genes that constitute a multi-genic chromosome:

~headsize = 8;
~numgenes = 2;

Then the the unit generators that are going to be included in the experiment are defined in an array. The following array contains the safest unit generators that are most likely to produce valid SynthDefs immediately. Including less stable UGens such as filters or delays causes more server compilation errors and it takes the algorithm considerably longer to find a valid set of individuals.

~ugens = [LFCub, LFPar, LFSaw, SinOsc, SinOscFB, Formant, LFGauss, LFTri, LFPulse, LFNoise1, LFNoise2, LFNoise0, 
	Blip, Saw, PMOsc, VarSaw, Impulse, SyncSaw, LFClipNoise];

The linker method determines how the genes that make up a multi-genic chromosome are linked together. In sound synthesis, the most common way to link two unit generator graphs is either by multiplication or addition. In this case we are using the former.

~linker = AbstractFunction.methods.select({arg meth; meth.name == '*' }).first;

The main object that handles the gene expression synthesis process, UGepRun, creates an initial population with 128 chromosomes. The ncoef parameter determines how many MFCC coefficients are used by the fitness function while comparing each individual in the population to the target statistics, rate determines the sampling rate of statistics in this case 20 per second. The targetBufPath parameter is the path to the example soundfile each candidate solution is compared to, you should bear in mind that the duration of this sound file determines the duration of analysis of each individual in the population, so choosing a file longer than 3-6 seconds will correspondingly increase the time it takes for the algorithm to iterate through all individuals. The methodRatio increases or decreases the relative number of unit generators as opposed to terminals in the head section of a gene. In this case, on the average 80% of codons are unit generators, which increases the overall nesting complexity of genes.

~run = UGepRun(
	size: 128,
	numgenes: ~numgenes,
	ncoef: 20,
	rate: 20,
	headsize: ~headsize,
	methods: ~ugens,
	linker: ~linker,
	targetBufPath: Paths.soundDir +/+ "gep/random.aif",
	forceArgs: nil,
	methodRatio: 0.8
);

Before the population can be evaluated for fitness, first we need to create target statistics and wait for this to complete until a line appears in the post window informing that resources have been freed.

~run.createTargetStats;

Once the target statistics have been created, we call the method that defines the fitness function.

~run.defineFitnessFunction;

At this point, the gene expression synthesis process is set up and ready to be executed. The first time around, the initial population is assigned fitness values by executing the assignScores method. This is only done once in the beginning of the experiment.

~run.assignScores;

Once this method is executed, you should wait until the method is finished looping through the population. You should see the algorithm print individual scores in the post window as it iterates through the population and assigns a score to each individual. The evaluation duration for each individual is determined by either the length of the target sound file or the fragdur parameter to the defineFitnessFunction method.

When the algorithm is finished iterating through the population, it recalculates scores based on CPU usage statistics measured during execution of each individual synth and normalized to the minimum and maximum values of the population to encourage resource efficiency. This introduces a tendency in the population towards simpler unit generator graphs and is countered by measuring the nesting depth of each expression tree and recalculating all scores to reward greater complexity. Once the scores have been adjusted for resource efficiency and complexity, the algorithm prints the maximum and mean scores of the population and we can listen to the results. We can listen to all of the individuals, but this is quite a time-consuming activity given the size of the population. Therefore a fitness threshold can be used to only select individuals with scores above that value. The threshold value depends entirely on the scores. In my experience, it ranges from 6.0 to 8.0 if I typically want to listen to approximately 30 individuals for each generation. The play method then loops through the selected individuals and prints relevant statistics to the post window as it progresses.

~th = 6.5;

~run.selectScores(~th).size;

~run.play(~th);

The gene expression synthesis library has built-in functionality to store the chromosomes, the metadata and the SynthDef to enable recalling generated synths or using their genotypes in other experiments as initial population. This functionality depends on the ZArchive quark. In order to choose to save any of the synthdefs to disk, add the index of the chromosome you want to store to this array as you are listening to the results (the index is the last part of the SynthDef name printed into the post window):

~saveArray = [];

Once the listening is finished, you can store the selected synthdefs, the parameters and the related metadata. If you have created the necessary directory structure, execute this line and wait for the process to complete to store the selected individuals.

~run.save(~saveArray);

When the save has finished, a new population of individuals can be generated by executing the .next method.

~run.next;

Once the new population of individuals has been created and each chromosome assigned a fitness score, return to determining the threshold value for the particular population based on the fitness values and repeat the listening, storing and next generation cycle as many times as desired (or until SuperCollider crashes)

The gene expression synthesis environment was developed to find a balance between theoretical research and practical application with an emphasis on the latter. This focus on evolving synthesizers for use in live performances has guided many design decisions in the development process and would not make as much sense if the focus was pure research. For example, implementing the fitness evaluation in non-real-time rendering mode would significantly speed up the experiments, however, since the interest was in being able to evolve the synthesizers in real time, this feature has not been implemented yet.

There is a repository of synthesizers evolved with gene expression synthesis on github which contains thousands of synthdefs and related metadata to be used in live performances. There are many practical applications for these synthesizers, that have been implemented in different projects. In f(x) the gene expression synthesizers have been added as additional textural sound sources controlled alongside the original layers created from recycled sonic material. The mikro system implements a set of these synthesizers as part of the sonic vocabulary of machine improvisers who make selections based on the audio analysis data stored in the repository. Recent live coding performances of sparsematrix have made use of synthesizers evolved for purpose to be computationally less expensive and have sonic characteristics more suitable for percussive envelopes. This is a video recording of an audiovisual live coding performance with Shelly Knotts at the live.code.festival in Karlsruhe in 2012 during which the tried and tested live coding tricks were supplemented by attempting to evolve synthesizers in real time:

This is an audio recording of a solo performance at the Music Hackspace in London using synthesizers exclusively evolved with gene expression synthesis:

The following few examples are taken from the online repository. All synthesizers have a unique identifier which also serves as a name for the SynthDef object. The identifier is comprised of the generation number, the individual's index in the population, and the time when it was stored into the repository. For example, the first SynthDef below was created on August 2 2013 at 20:39:37, its index in the population was 151 and it was part of the initial population of the run. The following four examples were all evolved in an experiment in which the head size of genes was defined as 16 and each multi-genic chromosome was comprised of 4 genes with multiplication serving as the linker function. There were a varying selection of unit generators used as is evident from the results, some of which are not in the standard distribution of SuperCollider. When playing these examples, please take care to start with low amplitude values and when there is no sound, chances are a NaN, inf or null value has occurred. It has not been established yet what the real impact of the execution context. These examples were evolved either in SuperCollider 3.5 on Mac OS 10.6.8 or SuperCollider 3.7alpha on Xubuntu 12.04.

(
~synth=SynthDef('gep_gen002_075_130802_203937', {|out=0,amp=0,a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y|  
Out.ar(out,Pan2.ar(Normalizer.ar(LeakDC.ar((  LFNoise1.ar( FMGrain.ar(h,  PMOsc.ar(y, e, l, b, u, x ),  
Dust2.ar(j, t, e ), y, p,  Ball.ar(n, v, v, n ), e ), l,  HenonL.ar( FMGrain.ar(n, n, w, d, j, d, i ), m, d,  
Blip.ar(b, v, u, x ),  FMGrain.ar(l, f, d, q, t, c, d ), j, n ) ))*( InGrain.ar( LFPulse.ar(r, u,  
Spring.ar( LFNoise2.ar(c, m, i ), j, f ), c,  CML0.ar(x, v, d, f, x, y ) ),  Pulse.ar( LFPulse.ar(b, p, j, t, g ), 
o, a,  InGrain.ar(q, p, s, r, n ) ), i, l, d ))*( CuspL.ar( Spring.ar( Logist0.ar( SawDPW.ar(k, j, s, c ),  
QuadL.ar(j, b, w, n, o, v, g ), p, a, w ),  Logist0.ar(e, x, g, u, i ),  Crackle.ar(x, d, m ) ),  LFDNoise0.ar( 
LFDNoise0.ar(x, i, w ), f,  LFDNoise0.ar(r, d, a ) ), p, p, o, t ))*( FMGrain.ar( Blip.ar(v,  CuspL.ar(l, w, f, y, 
g, e ),  LFTri.ar(j, w, i, u ),  SinGrain.ar(m, p, u, v, n ) ), w, w, g, f,  SinOsc.ar( LFDNoise0.ar(n, t, r ),  
PMOsc.ar(b, u, u, g, x, h ),  HenonL.ar(k, y, g, i, p, p, d ),  FMGrain.ar(p, d, p, b, a, b, y ) ), r ) ))),0,amp)) 
}).play(args: [ 'a', 1.6420102119446, 'b', 13.110636711121, 'c', -0.86799949407578, 'd', 0.027232756838202, 
'e', 0.56061327457428, 'f', 1.087641119957, 'g', 0.38823771476746, 'h', -0.25842821598053, 'i', 0, 
'j', 446.90447998047, 'k', 0.43448439240456, 'l', 1.1984220743179, 'm', -12.711162567139, 'n', 0.1513260602951, 
'o', 0.81048035621643, 'p', 0.97161960601807, 'q', 14.569178581238, 'r', 0, 's', 0.42289450764656, 
't', 0.17267155647278, 'u', 0.09271328151226, 'v', 1.4842553138733, 'w', 255.04020690918, 'x', 0.98315191268921, 
'y', 1.3111319541931 ]
)
)

~synth.set('amp', 0.3)

~synth.free

This individual was created 225th in the second generation on July 21, 2013 at 22:00:22, head size 16, number of genes 4, multiplication linker.

~synth=SynthDef('gep_gen002_225_130721_220022', {|out=0,amp=0,a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y|  
Out.ar(out,Pan2.ar(Normalizer.ar(LeakDC.ar((  Saw.ar(i, r,  Pulse.ar(t, h, i,  SinOsc.ar(y, r, i, p ) ) ))*
( StandardL.ar(m, h,  SawDPW.ar(s,  HenonL.ar(d, s, n, t, o, d, r ),  LFDNoise0.ar(r, f, p ),  Crackle.ar(e, v, h ) 
), a,  FMGrain.ar( LFSaw.ar(l, w, h, j ),  Pluck.ar(c, y, a, g, t, g, x, d ),  LFNoise2.ar(u, j, c ),  
LFNoise1.ar(h, y, s ), j, y, k ),  LFDNoise0.ar(a, e, b ) ))*( HPF.ar( LFNoise1.ar(p,  SyncSaw.ar(r,  
StandardL.ar(d, j, k, x, o, j ), g, n ),  GbmanL.ar( SinOsc.ar(j, b, c, d ), o, l, h, i ) ),  Saw.ar( 
HenonL.ar(e, p, q, y, n, p, l ),  Crackle.ar(w, r, h ),  Logist0.ar(n, r, a, g, g ) ), j, i ))*( SinOsc.ar(h, y, e,  
DelayL.ar(b,  SinGrain.ar(q, x,  LFPulse.ar(k, k, q, d, w ),  LFNoise2.ar(e, j, c ), h ), k, p, n ) ) ))),0,amp)) 
}).play(args: [ 'a', 1.8553959131241, 'b', 0.51838505268097, 'c', -0.0, 'd', 1.0, 'e', 1.3515774011612, 
'f', 13.44327545166, 'g', 100.0, 'h', 0.47877484560013, 'i', 0.19178818166256, 'j', 10.339004516602, 
'k', 0.62915289402008, 'l', 1.1528444290161, 'm', 1.712232708931, 'n', -99.176498413086, 'o', 0.30813097953796, 
'p', 1.6116172075272, 'q', 100.0, 'r', -0.922816157341, 's', 2.7296350002289, 't', 29.545949935913, 
'u', 0.84798073768616, 'v', 0.72206455469131, 'w', 0.61274516582489, 'x', 0.34379503130913, 
'y', -0.021308589726686 ]
)

~synth.set('amp', 0.3)

~synth.free

This individual was created 22nd in the initial generation on April 12, 2014 at 15:11:10, head size 12, number of genes 2, multiplication linker.

~synth=SynthDef('gep_gen000_022_140412_151110', {|out=0,amp=0,a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u|  
Out.ar(out,Pan2.ar(Normalizer.ar(LeakDC.ar((  LFNoise2.ar( LFDNoise1.ar(f,  Crackle.ar( StandardL.ar( 
LFPulse.ar(a, p, t, p, a ),  LFSaw.ar(a, s, l, d ), u, n, u, n ), m,  SyncSaw.ar(e, k, h, c ) ), c ), i, r ))*
( StandardL.ar( Pulse.ar( StandardL.ar(e, d, q, l, t, p ), t,  LFClipNoise.ar(p, f, j ),  LFCub.ar(h, q, m, f ) ),  
SawDPW.ar(r, r, p, e ),  LFCub.ar(e, p, p, u ),  StandardL.ar(h, p, e, t, b, f ), f,  Pulse.ar(c, l, s, s ) ) ))),
0,amp)) }).play(args: [ 'a', -inf, 'b', 7.5127568244934, 'c', 20000, 'd', 0.33801394701004, 'e', 221.58908081055, 
'f', 0.00026888391585089, 'g', 0.84298938512802, 'h', 2.8826158046722, 'i', 5.3661518096924, 'j', 45855.171875, 
'k', 0.86832499504089, 'l', 20000, 'm', 20000, 'n', 0.1672568321228, 'o', 1.0492409467697, 'p', 0.94249624013901, 
'q', 16107.75390625, 'r', 0, 's', 2.4334709644318, 't', 0, 'u', 222.01567077637 ]
)

~synth.set('amp', 0.3)

~synth.free

This individual was created 54th in the initial generation on February 7, 2014 at 18:54:45, head size 12, number of genes 2, multiplication linker.

(
~synth=SynthDef('gep_gen000_054_140207_185445', {|out=0,amp=0,a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s|  
Out.ar(out,Pan2.ar(Normalizer.ar(LeakDC.ar((  PMOsc.ar(d,  LFPulse.ar( LFClipNoise.ar(d, k, n ), o, q, r,  
LFCub.ar(q, g, i, n ) ),  Formant.ar(j, c, b, n, m ),  LFDNoise1.ar(j, m, i ), d, j ))*( Blip.ar(l, j, h, j ) ))),
0,amp)) }).play(args: [ 'a', 8.6660928726196, 'b', 0.55602639913559, 'c', 0.60943400859833, 'd', 0.2198121547699, 
'e', 1.6151390075684, 'f', 0.67369383573532, 'g', 12.028810501099, 'h', -0.73037302494049, 'i', 744.66326904297, 
'j', 0.25825279951096, 'k', 43.151161193848, 'l', 0, 'm', -1.8879414796829, 'n', 0.066980496048927, 
'o', 1.7984758615494, 'p', 0.16054487228394, 'q', 0.54126703739166, 'r', 0.8998036980629, 's', 745.94848632812 ]
)

~synth.set('amp', 0.3)

~synth.free

This individual was created 56th in the second generation on May 1, 2013 at 18:16:19, head size 12, number of genes 4, multiplication linker.

~synth=SynthDef('gep_gen001_056_130501_181619', {|out=0,amp=0,a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y|  
Out.ar(out,Pan2.ar(Normalizer.ar(LeakDC.ar((  SinOsc.ar(x, v, y, b ))*( Blip.ar(g, c,  LFTri.ar( LPF.ar( 
LFPar.ar(t, x, r, u ), t, r, q ),  SyncSaw.ar(r, s, h, d ),  LFTri.ar(l, h, v, i ), h ), l ))*( PinkNoise.ar( 
Pulse.ar(v, l,  CML0.ar( Impulse.ar(c, j, r, i ), e, c, x, t, o ),  LFPulse.ar(i, t, c, n, l ) ),  Crackle.ar(d, a,  
SinOsc.ar(i, v, l, u ) ) ))*( LFPulse.ar(w, f, c,  Saw.ar( Blip.ar(f, t, v, j ),  Crackle.ar(k, a, k ),  
PMOsc.ar(b, u, n, l, d, g ) ),  Blip.ar( LFNoise2.ar(a, w, d ),  Blip.ar(c, g, m, a ), s, r ) ) ))),0,amp)) 
}).play(args: [ 'a', 1.2730071544647, 'b', 0.77776551246643, 'c', -2.3435547351837, 'd', 1.5629274845123, 
'e', 7.3943738937378, 'f', 0.20331063866615, 'g', 3.0187730789185, 'h', 0.16514046490192, 'i', -0.2454995661974, 
'j', 0.20167124271393, 'k', 1, 'l', 0.23352435231209, 'm', 72.842254638672, 'n', -0.33126041293144, 
'o', 0.18563492596149, 'p', 0.67251986265182, 'q', -0.90473026037216, 'r', 0.31606477499008, 's', -99.631721496582, 
't', 72.272300720215, 'u', 0.3682769536972, 'v', 0.63806933164597, 'w', 2.6154305934906, 'x', 0.81047093868256, 
'y', -0.10205411165953 ]
)

~synth.set('amp', 0.3)

~synth.free

The following example shows how to use the gene expression synthesis loader and player objects to access and play synthesizers from the repository. This example only works if you have previously either built up a database of synthesizers or cloned the repository from github. Please note that the player class uses Joe Anderson's Ambisonic Toolkit which is available as a Quark. It is probably fairly straightforward to make it work without.

(
~headsize = 12;
~numgenes = 2;

~decoder = FoaDecoder(decoderType:'stereo');

~data = UGepLoader(~headsize, ~numgenes).load;

~foa = #[zoom,focus];
~player = GepPlayer(~data, ~decoder);

)

~decoder.start

~player.start(~foa)

~player.setFoa('zoom', 1.0)
~player.setFoa('focus', 1.0)

	
~indZoom = 14
~player.play(~indZoom, 0, 'zoom', 0)
~player.set(~indZoom, 0.1)

~player.setWithPattern(~indZoom, Pwhite(0.05, 0.2, inf), Pbrown(0.03125, 0.25, 0.03125, inf))

~player.free(~indZoom)